Question

how to solve this problem, find the variance. Round your answer to one decimal place. Previous answer: mean = 5.8.

Answer 1

To calculate the variance in this case, we need to use the variance for a discrete variable and its probability.

The equation we need to use in this case is:

`\sigma=\sum ^{}_i(x_i-\mu)^2P(x_i)`

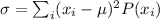
Where x_i is each value in the first row and P(x_i) is each value in the second row.

First, let's calculate each square difference:

`\begin{gathered} (4-5.8)^2=(-1.8)^2=3.24 \\ (5-5.8)^2=(-0.8)^2=0.64 \\ (6-5.8)^2=(0.2)^2=0.04 \\ (7-5.8)^2=(1.2)^2=1.44 \\ (8-5.8)^2=(2.2)^2=4.84 \end{gathered}`

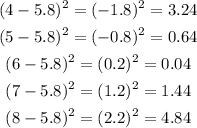
Now, we need to multiply each for its corresponding P(x):

`\begin{gathered} 3.24\cdot0.3=0.972 \\ 0.64\cdot0.2=0.128 \\ 0.04\cdot0.1=0.004 \\ 1.44\cdot0.2=0.288 \\ 4.84\cdot0.2=0.968 \end{gathered}`

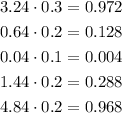
Finally, we sum them all to get the variance:

`\sigma=\sum ^{}_i(x_i-\mu)^2P(x_i)=0.972+0.128+0.004+0.288+0.968=2.360\approx2.4`

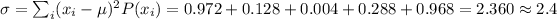
So, the variance to one decimal place is 2.4.