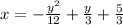1. Choose a point on the parabola
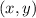
2. Find the distance from the focus to the point on the parabola.
![\sqrt[]{(x+1)^2+(y-2)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/xs9a089x3ida6elpi9zbgwd7b4v5yzbvpc.png)
3. Find the distance from the point on the parabola to the directrix.
![\sqrt[]{(x-5)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/70lnckxqa9f2vhjity5n5ojciovgcqr5uz.png)
4. Set the distance from the focus to the point equal to the distance from directrix to the point.
![\sqrt[]{(x+1)^2+(y-2)^2}=\sqrt[]{(x-5)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/1qap6ej8auolcthaamrxv8epzttozmuwb6.png)
5. Square both sides and simplify
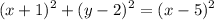
6. Write the equation of the parabola.