Hello there. To solve this question, we'll have to remember some properties about finding the common denominator of a sum of fractions.
Given the fractions:
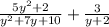
We start by factoring the expression in the denominator of the first fraction.
Notice it is something of the form x² - Sx + P, where S = -7 and P = 10.
S and P are the sum and the product of the roots of the expression. In this case, we can easily find values that would give us a sum of -7 and a product of 10:
y = -2 and y = -5
Thus, we write it as:
y² + 7y + 10 = (y + 2)(y + 5)
Then we have:
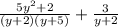
Now, to find the common denominator, we calculate the least common multiple of the expressions:
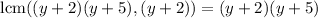
We can calculate it as:
Therefore this is the common denominator of the fractions, in its factored form.