The surface area of an sphere is given by the expression
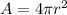
Since wer know the surface area, we can solve this expression for the radius, calculate it and then use it in the formula for volume given, as following:
![\begin{gathered} A=4\pi r^2\rightarrow(A)/(4\pi)=r^2 \\ \\ \Rightarrow r=\sqrt[]{(A)/(4\pi)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mhn9j0kprxji3dyqi9dqu14zjojx0t55f5.png)
![\rightarrow r=\sqrt[]{(484\pi)/(4\pi)}\rightarrow r=11](https://img.qammunity.org/2023/formulas/mathematics/college/zndnnm4r4xu88vtosis6vbbmgva3akerin.png)
![\begin{gathered} V=(4)/(3)\pi r^3 \\ \\ \rightarrow V=(4)/(3)\pi(11)^3 \\ \\ \Rightarrow V=1774.7\pi\operatorname{cm} \end{gathered}]()
Therefore, the correct answer is:
Option 2