Question

Please answer #10 that is shown in the picture below.

Answer 1

The given information is:

`\begin{gathered} \angle T=29 \\ \angle O=79 \\ DO=14 \end{gathered}`

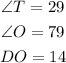
By applying the law of sines we have:

`(DO)/(\sin T)=(TD)/(\sin O)`

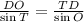
Replace the known values and solve for TD:

`\begin{gathered} (14)/(\sin29)=(TD)/(\sin79) \\ TD=(14*\sin79)/(\sin29) \\ TD=(14*0.98)/(0.48) \\ TD=28.35 \end{gathered}`

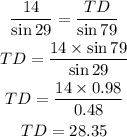
Side TD measures 28.35.

The sum of the interior angles of a triangle is always 180°.

Then D+O+T=180°.

By replacing the known values we can find D:

`\begin{gathered} \angle D+79+29=180 \\ \angle D=180-79-29 \\ \angle D=72 \end{gathered}`

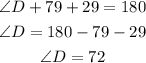
Angle D measures 72°.

And now we can apply the law of sines again:

`(DO)/(\sin T)=(OT)/(\sin D)`

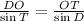
Replacing the known values:

`\begin{gathered} (14)/(\sin29)=(OT)/(\sin 72) \\ OT=(14*\sin 72)/(\sin 29) \\ OT=(14*0.95)/(0.48) \\ OT=27.46 \end{gathered}`

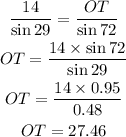
The side OT measures 27.46