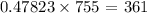361 light bulbs out of the 755 will last over 1330 hours
Here, we want to calculate the expected number of bulbs
The first thing we have to do here is to calculate the z-score
We have this as follows;
![\begin{gathered} z\text{ = }\frac{x-\mu}{\frac{\sigma}{\sqrt[]{n}}} \\ x\text{ = 1330 hours} \\ \mu\text{ = 1300 hours (mean)} \\ \\ \sigma\text{ = 20 hours ( standard deviation)} \\ n\text{ = 755} \\ \\ z\text{ = }\frac{1330-1300}{\frac{20}{\sqrt[]{755}}}\text{ = 0.0546} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/lg6ed3y43hpqb3o5andtc6gs3c72g5xb6n.png)
Now, we have to calculate the probability that is equal to this z-score
So, the probability we want to calculate is that which is greater than the calculated z-score
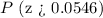
We are going to use the standard normal distribution table here
By using the table, we have the equivalent probability as 0.47823 (about 48%)
So, out of the 755 freshly installed light bulbs, 47.823% will last more than 1330 hours
The exact number that will last will be;