Question

Instructions: write the equation of the line graft below in point slope form used to red dots

Answer 1

y - 4 = -4(x+2)

Explanations:

The equation of a line in point-slope form is given as shown below;

`y-y_1=m(x-x_1)`

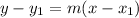
where;

m is the slope

(x1, y1) is any point on the line

Given the following parameters

(x1, y1) = (-2, 4)

Determine the slope of the line using the coordinates (0, -4) and (-2, 4)

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(4-(-4))/(-2-0) \\ m=(4+4)/(-2) \\ m=-(8)/(2) \\ m=-4 \end{gathered}`

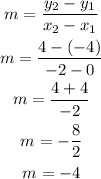
Substitute the slope and the point into the formula above to have:

`\begin{gathered} y-4=-4(x-(-2)) \\ y-4=-4(x+2) \end{gathered}`

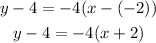
This gives the required equation in point-slope form