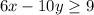
we simplify the expression to work easier
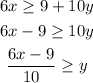
now we check each point replacing the coordinates and checking the inequality
A.
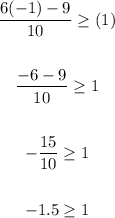
A is wrong because -1.5 isnt greater than 1 , so the inequality is wrong
B.
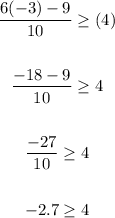
B is wrong because -2.7 isnt greater than 4
C.
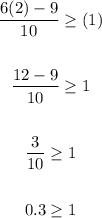
C is wrong because 0.3 isnt greater than 1
D.

D is right because 1.5 is grreater than -2
E.
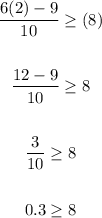
E is wrong because 0.3 isnt greater than 8
F.

F is Right because 2.1 is greater than 2