Question

Find the probabilities of the events below. Write each answer as single fraction

Answer 1

Answer:

Part A:

a) P(A) = 1/2 b) P(B) = 4/7 c) P(A and B) = 1/7 d) P(A or B) = 13/14 e) P(A or B) = 13/14

Part B:

P(A) + P(B) - P(A and B) = P(A or B) (last option)

Step-by-step explanation:

Given:

A Venn diagram of the 14 students in Ms. Patterson's class

To find:

Part A:

a) P(A) b) P(B) c) P(A and B) d) P(A or B) e) P(A) + P(B) - P(A and B)

Part B:

To find the probability equal to P(A) + P(B) - P(A and B)

a) P(A) = number students in A/total

Total students = 14

number of students in A = 7

P(A) = 7/14 = 1/2

b) P(B) = number students in B/total

number of students in B = 8

P(B) = 8/14 = 4/7

c) P(A and B) = number of students in A and B

P(A and B) = 2/14 = 1/7

d) P(A or B) = P(A) + P(B) - P(A and B)

`\begin{gathered} P(A\text{ or B\rparen = }(1)/(2)\text{ + }(4)/(7)\text{ - }(1)/(7) \\ P(A\text{ or B\rparen = }\frac{7(1)\text{ + 2\lparen4\rparen - 2\lparen1\rparen}}{14} \\ P(A\text{ or B\rparen}=\text{ }(7+8-2)/(14) \\ P(A\text{ or B\rparen = }(13)/(14) \end{gathered}`

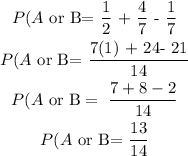
e) P(A) + P(B) - P(A and B) = P(A or B)

P(A) + P(B) - P(A and B) = 13/14

Part B:

P(A) + P(B) - P(A and B) = P(A or B) (last option)