Question

What's the approximate measure of one interior angle of the regular polygon shown?Question options:A) 220° B) 2.7° C) 1,620°D) 147.3°

Answer 1

Given:

Number of sides of the polygon, n = 11

Let's find the approximate measure of one interior angle of the polygon.

To find the measure of one interior angle, apply the formula:

`\text{ interior angle = }((n-2)*180)/(n)`

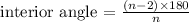
Where:

n = 11

Thus, we have:

`\begin{gathered} \text{ interior angle = }((11-2)*180)/(11) \\ \\ \text{ interior angle = }((9)*180)/(11) \\ \\ \text{ interior angle = }(1620)/(11) \\ \\ \text{ interior angle = }147.27\degree\approx147.3\degree \end{gathered}`

Therefore, the approximate measure of one interior angle of the regular polygon is 147.3 degrees.

ANSWER:

D) 147.3°