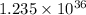The gravitational force between two point particles with masses M and m separated a distance r is given by Newton's Law of Universal Gravitation:
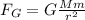
On the other hand, the electric force between two point particles with charges Q and q separated a distance r is given by Coulomb's Law:
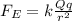
Where G is the gravitational constant and k is the Coulomb's constant:

Then, the ratio between the electric and gravitational forces between two particles with charge Q and q and mass M and m is:
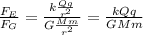
The mass and charge of a proton are:
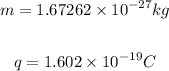
Replace both charges and both masses for those of a proton to find the ratio of the electric force to the gravitational force on one proton due to the other proton. Notice that the result of the ratio between the forces is the same independently of the distance between the protons:
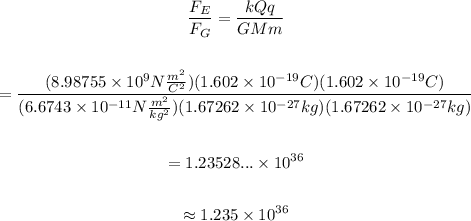
The electric force between two protons is 10^36 times stronger than the gravitational force between them.
Therefore, the answer is: