Question

Determine if a triangle can be formed with given length if yes classify as acute right or obtuseQuestion 3

Answer 1

Yes, a triangle can be formed with the given lengths.

The triangle will be obtuse.

Step-by-step explanation:

Given:

9, 40, 42

To find:

Determine if a triangle can be formed with the given lengths if yes classify as acute, right, or obtuse.

Recall that the Triangle Equality theorem states that for any triangle, the sum of lengths of any two sides must be greater than or equal to the length of the remaining side.

We can see that the sum of the two smallest side lengths 9 and 40 is 49 and 49 is greater than the length of the remaining side which is 42, so we can say that a triangle can be formed from the given lengths.

To determine if the triangle is acute, right or obtuse we'll go ahead and determine the sum of the squares of the two smaller side lengths and compare it with the square of largest side length;

`\begin{gathered} 9^2+40^2=81+1600=1681 \\ 42^2=1764 \\ 1681<1764 \end{gathered}`

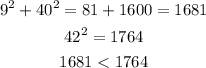
Since the sum of the squares of the smaller side lengths is less than the square of the largest side length, so the triangle is obtuse