SOLUTION:
Step 1:
In this question, we are asked to find the equation of the circle with the given characteristics in standard form:
Step 2:
We need to get the distance between the two points:
(11 , - 7 ) and ( 17 , 13 )
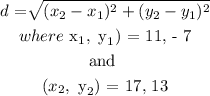
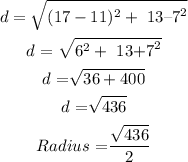
Next:
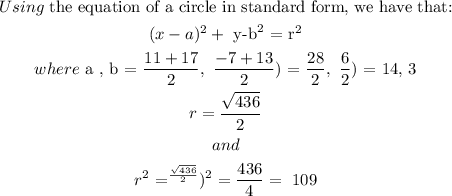
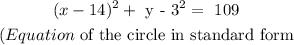
The graph is as follows: