Question

A research institute poll asked respondents if they felt vulnerable to identity theft. In the poll, n=1086 and x=571 who said "yes." Use a 99% confidence level. A) Construct the confidence interval._ < p <_ (round to three decimal places.)

Answer 1

The given information is:

n=1086

x=571

Confidence level 99%

First, we need to find the sample proportion. It is given by the formula:

`\hat{p}=(x)/(n)`

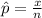
By replacing the known values, we obtain:

`\hat{p}=(571)/(1086)=0.526`

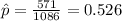
Now, the confidence interval is given by:

Now, replace this value into the formula and solve:

`\begin{gathered} E=2.576\sqrt{(0.526(1-0.526))/(1086)} \\ \\ E=2.576\sqrt{(0.249)/(1086)} \\ \\ E=2.576√(0.0002) \\ \\ E=2.576*0.015 \\ \\ E=0.039 \end{gathered}`

The confidence interval is then:

[tex]\begin{gathered} 0.526-0.039

The answer is above.