Question

The volume of the square pyramid is ___ cubic meters.

Answer 1

The volume of a pyramid is equal to one-third of the product of the base area and the height, following the formula:

`V=(1)/(3)A_{\text{base}}\cdot h`

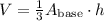
Since the base of the pyramid is a square, the area of its base is equal to the square of its side length:

`A_{\text{base}}=a^2`

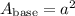
Then, you can write the formula for the volume as follows:

`V=(1)/(3)a^2h`

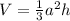
The side length of the base is a=30m and the height of the pyramid is h=20m, replace both values on the formula to calculate the volume:

`\begin{gathered} V=(1)/(3)\cdot(30^2)\cdot20 \\ V=(1)/(3)\cdot900\cdot20 \\ V=(1)/(3)\cdot18000 \\ V=6000m^3 \end{gathered}`

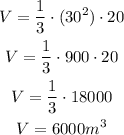
The volume of the square pyramid is 6000m³