Question

A theater group made appearances in two cities. The hotel charge before tax in the second city was $500 higher than in the first. The tax in the first city was 8.5%, and the tax in the second city was 7.5%. The total hotel tax paid for the two cities was $917.50. How much was the hotel charge in each city before tax?First city:Second city:Solve by tax rate or interest rate using system of linear equations.

Answer 1

• First city: $5,500

,

• Second city: $6,000

Explanation:

• Let the hotel charge before tax in the first city = x

,

• Let the hotel charge before tax in the second city = y

The hotel charge before tax in the second city was $500 higher than in the first.

`y=x+500\cdots(1)`

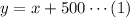
The tax in the first city was 8.5%, and the tax in the second city was 7.5%.

The total hotel tax paid for the two cities was $917.50.

`\begin{gathered} (8.5\%\text{ of x\rparen+\lparen7.5\% of y\rparen=917.50} \\ 0.085x+0.075y=917.50\cdots(2) \end{gathered}`

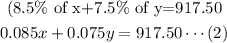
The problem gives rise to the system of linear equations below:

The system is then solved for x and y.

Substitute equation (1) into equation (2):

Finally, solve for y:

`\begin{gathered} y=x+500 \\ =5500+500 \\ =\$6,000 \end{gathered}`

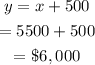
The hotel charge before tax in each city was:

• First city: $5,500

,

• Second city: $6,000