Given:
The perimeter of the rectangle, P=64 units.
From the figure, the length of the rectangle, l=PQ=3x+3.
The breadth of the rectangle, b=PS=2x-1.
Now, the expression for the perimeter of the rectangle can be written as,
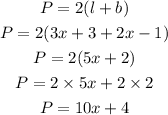
Now, put P=64 in the above equation and solve for x.
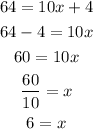
Now, we know b=PS=2x-1.
Hence, PS can be calculated as,
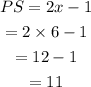
Therefore, the length of side PS is 11 units.