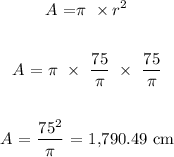The area of the circle is 1790.49 centimeters square
To calculate the area of the circle, we shall need the radius of the circle
We can get the radius from the arc length
Mathematically, the length of an arc is;

From the question, the length is 15 cm while the central angle is 36
Thus we have;

Mathematically, the area of the circle will be;