Question

At what x-values do the graphs of the functions y = cos 2x and y =3cos^2x-sin^2x intersect over the interval -pi

Answer 1

To find:

The x-values at the intersection of the graphs of two functions.

Solution:

Two functions are:

`y=\cos2x\text{ and }y=3\cos^2x-\sin^2x`

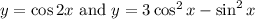
The functions are equal at the intersection. So,

`\cos2x=3\cos^2x-\sin^2x`

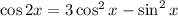
The solutions of the above equation are the x-values of the intersection.

`\begin{gathered} \cos2x=3\cos^2x-\sin^2x \\ \cos^2x-\sin^2x=3\cos^2x-\sin^2x \\ 2\cos^2x=0 \\ \cos^2x=0 \\ \cos x=0 \end{gathered}`

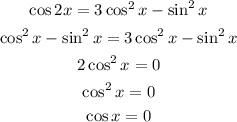
The solution to the above equation is:

`x=(\pi)/(2)+2\pi n\text{ and }x=(3\pi)/(2)+2\pi n`

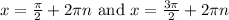
It is given that x lies between -pi and pi. So, the value of n = 0 for the first solution and n = 1 for the second solution. Therefore,

`x=(\pi)/(2)\text{ and }x=-(\pi)/(2)`

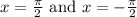
Thus, options A and B are correct.