1 Answer

Joe Fernandez · Answer 1 · 2023-12-21T10:58:07+0000

Step-by-step explanation:

Limit of the function:

Limit is the approximate value of the function at a defined value of x.

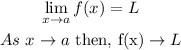
$\begin{gathered} \lim _(x\to a)f(x)=L \\ As\text{ }x\rightarrow a\text{ then, f(x)}\rightarrow L \end{gathered}$

a)

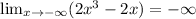
$\lim _(x\to-\infty)(2x^3-2x)=-\infty$

This limit is true. As x approaches negative infinity the function is also approached to negative infinity.

b)

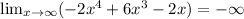
$\lim _(x\to\infty)(-2x^4+6x^3-2x)=-\infty$

As x tends to infinity. The functions tend to have negative infinity.

This statement is true.

c)

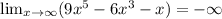
$\lim _(x\to\infty)(9x^5-6x^3-x)=-\infty$

When x tends to infinity, the function will also go to infinity.

So, This statement is false.

Please log in or register to add a comment.