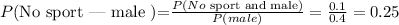Question

A panel for a political forum is made up of 11 people from three parties, all seated in a row. The panel consists of 5 Republicans, 5 libertarians, and I GreenParty member. In how many distinct orders can they be seated if two people of the same party are considered identical (not distinaX?

Answer 1

So,

Here we have the following table:

We want to find the probability to choose a man. So, there are 7+21 = 28 men in total.

The total number of people is 70, so this probability is:

`P(\text{male)}=(28)/(70)=0.4`

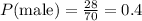
b) The probability that the person is a man who doesn't practice sport.

If we look at the table, there are 7 men who doesn't practice sport, so:

`P(no\text{ sport and male)=7/70}`

7/70 = 0.1, so this probability is 0.1

c) Finally, remember that:

`P(A|B)=(P(A\cap B))/(P(B))`

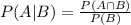
We want the to find the probability that the person doesn't practice sport given that it is a man.

If we replace:

`P(\textNo sport \frac{P(No\text{ sport and male)}}{P(male)}=(0.1)/(0.4)=0.25`