Question

Find the sum and classify the polynomial based on degree and number of terms.

Answer 1

We need to simplify the given expression as follows:

`\begin{gathered} 3n^2(5n^2-2n+1)+(4n^2-11n^4-9) \\ =(15n^4-6n^3+3n^2)+(4n^2-11n^4-9) \\ =4n^4-6n^3+7n^2-9 \end{gathered}`

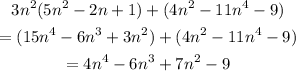
Now, to determine the degree of the polynomial we need to find the term which has the biggest exponential term. In this case, it is 4n^4. So, the expression is a 4th-degree polynomial.

Then, the answer is option C. 4th degree polynomial with 4 terms