Given the word problem, we can deduce the following information:
1. One month Lucy rented 3 movies and 5 video games for a total of $39.
2. The next month she rented 9 movies and 7 video games for a total of $63.
To determine the rental cost for each movie and each video game, we first let:
m= Rental cost for each movie
v= Rental cost for each video game
Hence, the linear equations would be:

We solve for m in 3m+5v=39:
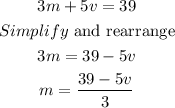
Next, we plug in the value of m into 9m+7v=63:
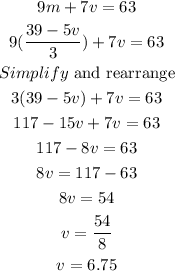
Then, we plug in v=6.75 into m=(39-5v)/3:

Therefore,
Rental cost for each movie = $1.75
Rental cost for each video game= $6.75