Question

A triangular pyramid with an equilateral base has a side length of 10 centimeters and a surface area of 214.5 square centimeters. Find its slant height. No photo given.

Answer 1

the The Solution:

Step 1:

We shall split the triangular pyramid into its component surfaces.

3 triangles + 1 triangle.

Step 2:

We shall find the area of the triangle in fig 1., by using Heron's formula.

`\begin{gathered} A=\sqrt[]{s(s-a)(s-b)(s-c)} \\ \text{Where A= area} \\ a=10\text{ ; b= 10 ; c=10} \\ s=(a+b+c)/(2)=(10+10+10)/(2)=(30)/(2)=15 \\ So, \\ A=\sqrt[]{15(15-10)(15-10)(15-10)} \\ A=\sqrt[]{15*5*5*5} \\ A=25\sqrt[]{3}cm^2 \end{gathered}`

Step 3:

We shall state the formula for calculating the total surface area of the triangular pyramid.

`\begin{gathered} \text{SA = Area of fig1 triangle + 3(}(1)/(2)bh) \\ \text{Where SA =surface area =214.5 cm}^2 \\ \text{Area of fig 1 triangle = 25}\sqrt[]{3}cm^2 \\ b\text{ =base =10 cm} \\ h=\text{slant height =?} \end{gathered}`

Step 4:

We shall substitute the above values into the formula.

`\begin{gathered} 214.5=25\text{ }\sqrt[]{3}\text{ + 3(}(1)/(2)*10* h) \\ 214.5=25\text{ }\sqrt[]{3}+3(5h) \\ 214.5=43.3+15h \\ \text{Collecting the like terms, we get} \end{gathered}`
`\begin{gathered} 214.5-43.3=15h \\ \text{Dividing both sides by 15, we get} \\ 171.2=15h \\ h=(171.2)/(15) \\ h=11.413\approx11.4\text{ cm} \end{gathered}`

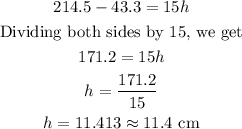
Step 4:

The presentation of the Answer.

The slant height is 11.4 centimeters.

Thus, the correct answer is 11.4 centimeters.