We are asked to find the density of the metal cone.
The density of a body is given by:
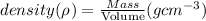
We have been given the Mass of the body as 2500 grams
All we need to find is the volume in order to find the density of the metal
The metal is a cone. The volume of a cone is given by:
![\begin{gathered} \text{Volume}=(1)/(3)*\pi* r^2* h \\ \\ r=\text{radius}=5\operatorname{cm} \\ h=height=20\operatorname{cm} \end{gathered}]()
Now we can find the volume of the metallic cone:
![\text{Volume}=(1)/(3)*\pi*5^2*20=523.599\operatorname{cm}^3]()
We have been given the mass of the cone and we just finished calculating the volume of the metal, therefore, we can find the density of the metal as:
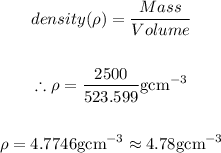
Therefore, the final answer is: 4.78g/cubic