Given:
Sandra's scores on the first four tests:
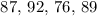
To have a mean score of at least 85 means that Sandra must have an average score of at least 85 on here 5 tests.
To get that, we will be using the following equation:
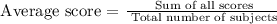
Total number of subjects: 5
Our target mean (average) score: 85
Let,
x = the missing score needed to get a mean score of at least 85.
We get,
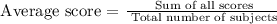
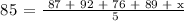
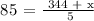
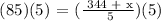
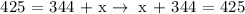
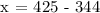
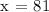
Therefore, for Sanda to get a mean test score of at least 85, she must get a minimum score of 81 on her fifth test.
The answer is 81.