Question

The perimeter of a rectangular garden is 110 feet. Find its dimensions if the length is 5 feet less than twice the width.

Answer 1

For this you can start by making a drawing

Since the perimeter is the sum of all the sides of a geometric figure then you would have

`\begin{gathered} x+y+x+y=110 \\ 2x+2y=110\rightarrow(1) \end{gathered}`

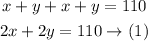
On the other hand, since the length of the rectangular garden is 5 feet less than twice the width, then

`\begin{gathered} x=2y-5 \\ \text{ Substract 2y from both sides of the equation} \\ x-2y=-5\text{ }\rightarrow(2) \end{gathered}`

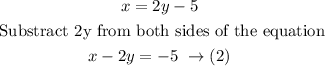
Now, with (1) and (2) you have a system of linear equations. To solve it you can use the elimination method, like this

`\begin{gathered} \mleft\{\begin{aligned}2x+2y=110 \\ x-2y=-5\end{aligned}\mright. \\ \text{Add both equations} \\ 3x+0y=105 \\ 3x=105 \\ \text{ Divide both sides of the equation by 4} \\ (3x)/(3)=(105)/(3) \\ x=(105)/(3)=35 \end{gathered}`

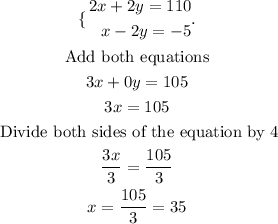
Finally to find the value of y, you can replace the value of x in (1) or in (2). For example in (1)

`\begin{gathered} 2x+2y=110 \\ 2(35)+2y=110 \\ 70+2y=110 \\ \text{ Subtract 70 from both sides of the equation} \\ 70+2y-70=110-70 \\ 2y=40 \\ \\ \text{ Divide both sides of the equation by 2} \\ (2y)/(2)=(40)/(2) \\ y=20 \\ y=20 \end{gathered}`

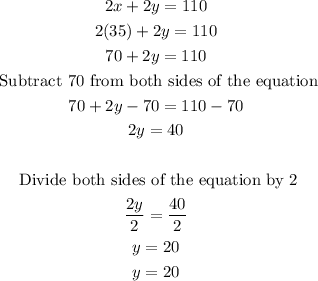
Therefore, the dimensions of the rectangular garden are 35 feet length and 20 feet width.