Question

A rope is 60 inches in length must be cut into two pieces one piece must be twice as long as the other find the length of each piece round your answers to the nearest inch if necessary

Answer 1

Let x be the length of one piece and y be the length of the other piece. Then, we can write:

`x+y=60\ldots(A)`

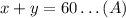
since one piece must be twice long than the other, we can write

`2x=y\ldots(B)`

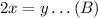
and we have 2 equations in 2 unknows.

Solving by substitution method.

By substituting equation B into equation A, we get

`x+(2x)=60`

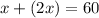
which gives

`\begin{gathered} 3x=60 \\ x=(60)/(3) \\ x=20 \end{gathered}`

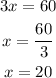
Now, in order to obtain y, we must substitute this result into equation B. It yields

`\begin{gathered} y=2x\Rightarrow y=2(20) \\ y=40 \end{gathered}`

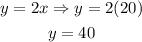
Therefore, the answer is x= 20 inches and y= 40 inches.