Answer: B) no
==========================================================
Step-by-step explanation:
The interval we're working with is [4,5] aka
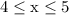
We'll plug the endpoints of said interval into the f(x) function
Let's start with x = 4
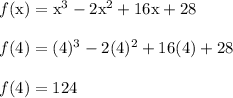
The actual result doesn't matter. All we care about is if the value is positive or negative. We see that f(4) is positive.
Now plug in x = 5
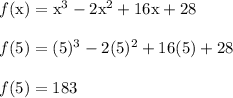
The value of f(5) is positive as well.
Unfortunately we don't have enough info to determine if f(x) has a root in the interval [4,5]
We would need either of the following conditions
- f(4) negative and f(5) positive
- f(4) positive and f(5) negative
In other words, we need the signs of f(4) and f(5) to alternate. One needs to be positive, the other negative. This is to guarantee that the f(x) curve crosses the x axis at some point. Think of it like a river or a road. The continuous road can't magically jump over the x axis without crossing it.
But because f(4) and f(5) don't differ in sign, this means we don't know if f(x) ever dips below the x axis. It might as shown in figure 1, but it may not as indicated in figure 2. There's simply not enough information.