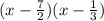1) the initial expression is:
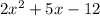
To factor this expression we can use the cuadratic formula that is:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4(a)(c)}}{2(a)} \\ a=2 \\ b=5 \\ c=-12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/34syktmfjk8caep2stpy1lz3j544dt04bp.png)
so we replace the values and we get:
![\begin{gathered} x=\frac{-5\pm\sqrt[]{5^2-4(2)(-12)}}{2\cdot2} \\ x=\frac{-5\pm\sqrt[]{121}}{4} \\ x=(-5\pm11)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ph878xodqi9yy5y3txcs7bc9qvfjmbxuw2.png)
So now we have two solutions so:
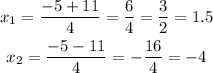
so the factor expression will be:
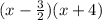
2) the initial expression is:
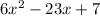
so we repeat the same procedure so:
![\begin{gathered} x=\frac{23\pm\sqrt[]{23^2-4(6)(7)}}{2(6)} \\ x=\frac{23\pm\sqrt[]{529-168}}{12} \\ x=\frac{23\pm\sqrt[]{361}}{12} \\ x=(23\pm19)/(12) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mokwxv1jhuz073bw5cag4pe9ad2mvhep35.png)
So the two possible solutions are:
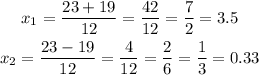
so the factor form is: