Question

A grocer wants to mix two kinds of coffee. One kind sells for $1.20 per pound, and the other sells for $2.35 per pound. He wants to mix a total of 24 pounds and sell it for$1.65 per pound. How many pounds of each kind should he use in the new mix? (Round off the answers to the nearest hundredth.)

Answer 1

Let be "x" the amount of coffee that is sold for $1.20 per pound (in pounds) that the grocer should use in the new mix and "y" the other kind of coffee that is sold for $2.35 per pound (in pounds) that the grocer should use in the new mix

Using the information given in the exercise, you can set up the following System of equations:

`\begin{cases}x+y=24 \\ 1.20x+2.35y=24\cdot1.65\end{cases}`

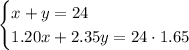
Simplifying, you get:

`\begin{cases}x+y=24 \\ 1.20x+2.35y=39.6\end{cases}`

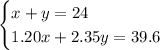
You can solve the system as follows:

1. Multiply the first equation by -1.20.

2. Add the equations.

3. Solve for "y".

Then:

`\begin{gathered} \begin{cases}-1.20x-1.20y=-28.8 \\ 1.20x+2.35y=39.6\end{cases} \\ ------------- \\ 1.15y=10.8 \\ y=9.39 \end{gathered}`

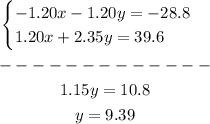
4. Substitute the value of "y" into the first equation.

5. Solve for "x".

Then:

`\begin{gathered} x+9.39=24 \\ x=24-9.39 \\ x\approx14.61 \end{gathered}`

Therefore, the answer is: About 14.61 pounds of the kind of coffee that is sold for $1.20 and about 9.39 pounds of the other kind of coffee that is sold for $2.35 per pound.