Answer:
Proportion of the adult men less than 6 feet tall = 74.857%
Explanations:
The mean height, μ = 70 inches
The standard deviation in height, σ = 3 inches
Proportion of the adult men less than 6 feet
1 foot = 12 inches
6 feet = 12 x 6 = 72 inches
x = 72 inches
Calculate the z-value using the formula below:
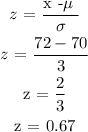
Probability that an adult men will be less than 72 inches (6 feet) tall
P(x < 72) = P(z < 0.67) = 0.74857
Therefore, proportion of adult men less than 72 inches (6 feet) tall = 0.74857 x 100% = 74.857%