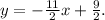To answer this question we will use the quotient rule for derivatives:

We know that:
![\begin{gathered} (\sqrt[]{x})^(\prime)=\frac{1}{2\sqrt[]{x}}, \\ (5x-6)^(\prime)=5. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a9bde2h1ju74sioe60omcd39yqz1zw91xv.png)
Then:
![f^(\prime)(x)=\frac{\frac{1}{2\sqrt[]{x}}\cdot(5x-6)-\sqrt[]{x}\cdot5}{(5x-6)^2}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/1vs9pcy9xllufwya8dbr69m8uf7zmt3r29.png)
Therefore, the slope of the tangent line to the graph of f(x) at (1,f(1)) is:
![f^(\prime)(1)=\frac{\frac{1}{2\sqrt[]{1}}(5\cdot1-6)-\sqrt[]{1}\cdot5}{(5\cdot1-6)^2}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/pwp12b2vduz8eyhbiolxveo1eej45et9ts.png)
Simplifying the above result we get:
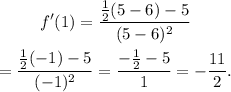
Now, we will use the following slope-point formula for the equation of a line:
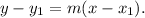
Therefore the slope of the tangent line to the graph of f(x) at (1,f(1)) is:
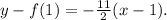
Now, we know that:
![f(1)=\frac{\sqrt[]{1}}{5\cdot1-6}=(1)/(5-6)=(1)/(-1)=-1.](https://img.qammunity.org/2023/formulas/mathematics/college/pbetink6seywv2cmkdch96yz7u0m3wvaez.png)
Therefore:
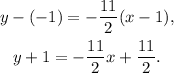
Subtracting 1 from the above equation we get:
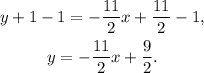
Answer: