Question

The lines represented by the equations y + 3x = 9 and y 5x + 1 are O parallel Submit Answer O perpendicular O the same line O neither parallel nor perpendicular

Answer 1

To know the relation between the lines we have to calculate the slope with this expression:

`y=mx+c`

whre m is the slope and c the intersection with the y axis, so for the first line

`\begin{gathered} y=-3x+9 \\ m=-3 \end{gathered}`

and for the secon line:

`\begin{gathered} y=-(1)/(3)x+1 \\ m=-(1)/(3) \end{gathered}`

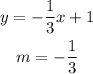
The slope is diferent, so they are not parallel, and they are not the same line. is they where perpendicular the slope of the second line should be the negative reciprocal of the first line. and in this case:

`-3\to(1)/(3)`

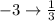
so they are not perpendicular. So the solution is numeral D) neither parallel nor perpendicular​