Question

Find the x-coordinate and y-coordinates of the center of gravity (as a multiple of a)

Answer 1

• x = 0.944a

,

• y = 1.333a

Step-by-step explanation

x- coordinate

The x-coordinate of each pair of piled blocks are:

• x₁ = x₂ = a/2

,

• x₃ = x₄ = 3a/2

The weights of the blocks are:

• W₁ = 20N

,

• W₂ = 80N

,

• W₃ = 70N

,

• W₄ = 10N

The total weight is the sum of the individual weights,

`W=W_1+W_2+W_3+W_4=20N+80N+70N+10N=180N_{}`

By the definition of center of gravity, the x-coordinate is,

`x_(cg)=\frac{\sum ^{}_iW_ix_i}{W}=((W_1+W_2)x_1+(W_3+W_4)x_3)/(W)`

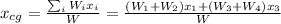
Replace with the values and solve,

`x_(cg)=((20N+80N)\cdot(a)/(2)+(70N+10N)(3a)/(2))/(180N)=(50a+120a)/(180a)=(170)/(180)a=0.944a`

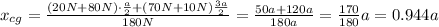
y- coordinate

The same equations apply to the y-coordinate. The y-coordinates of each weight are:

• y₁ = y₄ = a/2

,

• y₂ = y₃ = 3a/2

The y-coordinate of the center of gravity is,

`y_(cg)=\frac{\sum ^{}_iW_iy_i}{W}=\frac{(W_1+W_4)y1_{}+(W_2+W_3)y_2}{W}`

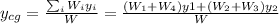
Replace with the values and solve,

`y_(cg)=\frac{(20N+10N)(a)/(2)_{}+(80N+70N)(3a)/(2)}{180N}=(15a+225a)/(180)=(240a)/(180)=1.333a`

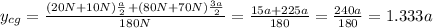
Hence, the coordinates of the center of gravity are (0.944a, 1.333a).