It is given that the base and height of parallelogram is (x-7)meters and (x+9)meters
The area is 92 square meters so it follows:
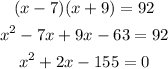
Solve the quadratic equation by the formula to get:
![\begin{gathered} x=\frac{-2\pm\sqrt[]{4-4*-155*1}}{2} \\ x=\frac{-2\pm\sqrt[]{624}}{2} \\ x=-1\pm2\sqrt[]{39} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h6ufd9asutocceutfs4rnyfxt1y11z8ov3.png)
Since the length is positive, the value of x is:
![x=-1+2\sqrt[]{39}](https://img.qammunity.org/2023/formulas/mathematics/college/505ghuxwqj6e047r31sgc4p4m3f6efifku.png)
So the value of the base and height are:
![\begin{gathered} x-7=-1+2\sqrt[]{39}-7\approx4.9 \\ x+9=-1+2\sqrt[]{39}+9\approx20.49 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/olqt1mdecvv6rp2cgx7smc56xwxs3tts7b.png)
Hence the base is 4.9 meters and the height is 20.49 meters.