a. Let the cost of an adult ticket be x and Let the cost of an children's ticket be y
We can deduce that;

Also Mrs. Ramirez paid 53.75 for 2 adult tickets and 3 children tickets, so;
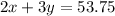
We can solve this simultaneously for x and y.
So, we have;
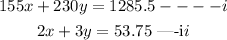
Let's make x the subject of the relation, we have

Let us substitute this relation for x in equation i
![undefined]()