Question

A board that is 35 inches long is cut into two pieces the longer piece is four times longer than the other piece how long are the pieces

Answer 1

The length of the pieces are:

X = 28

Y = 7

SOLUTION

Problem Statement

The question tells us about a board 35 inches long that is cut into two pieces with one piece being 4 times longer than the other.

We are then asked to find the length of the pieces.

Solution

To solve this question, we shall analyze the sentences in the question and form 2 separate equations that we will solve simultaneously.

Step 1:

The first statement is: "A board that is 35 inches long is cut into two pieces "

This statement implies that if the first piece is X and the second piece of the board cut out is Y, then, placing these two pieces side by side at the point where they are cut, should give us the full length of 35 inches again.

We can represent this information mathematically,

`X+Y=35\text{ (Equation 1)}`

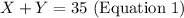
Step 2:

The second statement to consider is "the longer piece is four times longer than the other piece"

This statement implies that one of either X or Y is 4 times longer than the other. Choosing X as the longer piece length (anyone you choose would yield the same result). This means we can interpret this line mathematically as well,

`\begin{gathered} X=4Y\text{ (Equation 2)} \\ \text{That is, X is 4 times the length, Y} \end{gathered}`

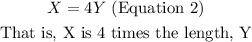
Step 3

Now that we have the two equations, we can solve them simultaneously. We will use the substitution method to solve. We already have variable X in terms of variable Y in Equation 2. Thus, all we just need to do is to substitute this expression for X into Equation 1.

This is done below:

`\begin{gathered} X=4Y\text{ (Equation 2)} \\ \text{substituting this expression for X into Equation 1} \\ X+Y=35\text{ (Equation1)} \\ 4Y+Y=35 \\ 5Y=35 \\ \text{Divide both sides by 5} \\ (5Y)/(5)=(35)/(5) \\ \therefore Y=7 \end{gathered}`

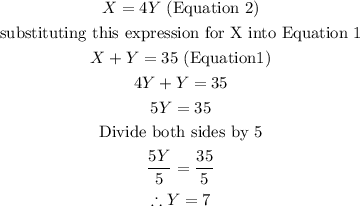
Now that we have the value of Y, let us substitute the value of Y into Equation 1 to find the value of X

`\begin{gathered} X+Y=35\text{ (Equation 1)} \\ \text{But we know that Y = 7,} \\ \\ X+7=35 \\ \text{Subtract 7 from both sides} \\ X+7-7=35-7 \\ \therefore X=28 \end{gathered}`

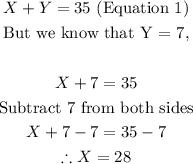
Final Answer

The length of the pieces are:

X = 28

Y = 7