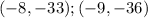Given the following System of equations:
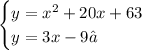
You can apply the following procedure to solve it:
1. Make the equations equal to each other:
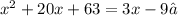
2. Solve for the variable "x":
- Make the equation equal to zero:
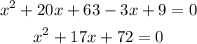
- You need to use the Quadratic formula to find the values of "x". This is:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
In this case:
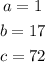
Substituting values and evaluating, you get:
![\begin{gathered} x=\frac{-17\pm\sqrt[]{17^2-4(1)(72)}}{2(1)} \\ \\ x=\frac{-17+\sqrt[]{1}}{2} \\ \\ x=\frac{-17-\sqrt[]{1}}{2} \\ \\ x=-8;x=-9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ut407lpcnfscvu0mfov7u9r2a0zeiq8iru.png)
3. Substitute each value of "x" into the second original equation and evaluate in order to find the corresponding values of "y":
- For:

You get:
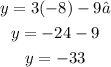
- For:

You get:
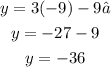
The points are: