Question

The length of the longer leg of a right triangle is 13 cm more than three times the length of the shorter leg. The length ofthe hypotenuse is 14 cm more than three times the length of the shorter leg. Find the side lengths of the triangle.

Answer 1

To answer this question we draw a diagram to help us:

In this diagram we let x be the length of the shorter leg, then we use the information given. Now using the pythagorean theorem we get the equation:

`(3x+14)^2=(3x+13)^2+x^2`

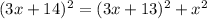
Solving for x we have:

`\begin{gathered} (3x+14)^2=(3x+13)^2+x^2 \\ 9x^2+84x+196=9x^2+78x+169+x^2 \\ x^2+78x+169-84x-196=0 \\ x^2-6x-27=0 \\ (x-9)(x+3)=0 \\ \text{then} \\ x=9 \\ or \\ x=-3 \end{gathered}`

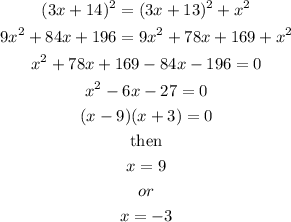
Since x is a lenght and lengths can't be negative we conclude that x=9. Once we know the value of x we plug it on the expression for the larger leg and the hypotenuse.

For the larger leg we have:

`3(9)+13=40`

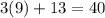
For the hypotenuse we have:

`3(9)+14=41`

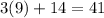
Therefore we conclude that:

Small leg is 9

Large leg is 40

Hypotenuse is 41