Recall the following types of factoring:
Difference of squares into a product of conjugate binomials:
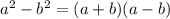
Quadratic equation without a constant term into the product by a common factor:
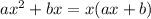
Perfect square trinomial into a binomial squared:
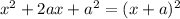
Notice that the first expression is a difference of the squares of 4x and 3. Then:
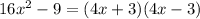
Then, the match for the first equation is Difference of squares.
The second expression has a common factor of 8x:
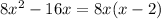
Then, the match for the second equation is GCF (greatest common factor).
The third expression is a perfect square trinomial:
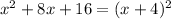
Then, the match for the third equation is Perfect Square Trinomial.