Step-by-step explanation
The equation of a line in slope-intercept form looks like this:

Where m is known as the slope. All lines that have the same slope m are parallel whereas a line perpendicular to y=mx+b has a slope given by -1/m.
In this case we have the line 5x-6y=1. We should write it in slope-intercept form. In order to do this we can add 6y to both sides and substract 1 from both sides:
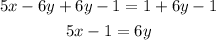
Then we divide both sides by 6:

Then the slope of this line is 5/6.
Answer
Following what we stated above we have these answers:
The slope of a line parallel to this is 5/6.
The slope of a line perpendicular to this is -6/5.