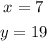Question

You have a combined 26 dimes and quartersThe total value of the coins is $5.45. How many of each type of coin do you have

Answer 1

Answer: There are;

7 Dimes and 19 Quarters

`\begin{gathered} x=7 \\ y=19 \end{gathered}`

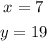
Step-by-step explanation:

Let x and y represent the number of each type of dime and quarter you have respectively.

Given that you have a combined 26 dimes and quarters.

`x+y=26\text{ ------ 1}`

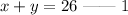
Also, recall that;

`\begin{gathered} 1\text{ dime = \$0.10} \\ 1\text{ quarter = \$0.25} \end{gathered}`

Given that the total value of the coins is $5.45.

`0.10x+0.25y=5.45\text{ -------- 2}`

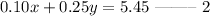
Solving the set equations.

multiplying equation 2 by 4;

and subtract from equation 1.

`\begin{gathered} 0.10x+0.25y=5.45\text{ -------- 2} \\ *4 \\ = \\ 0.40x+y=21.8 \\ \\ x+y=26 \\ - \\ 0.40x+y=21.8 \\ = \\ 0.60x+0=4.2 \\ x=(4.2)/(0.6) \\ x=7 \end{gathered}`

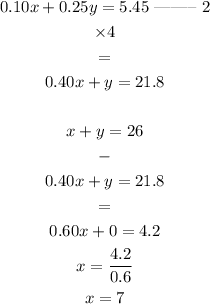
so, we can substitute the value of x into equation 1 to get y;

`\begin{gathered} 7+y=26 \\ y=26-7 \\ y=19 \end{gathered}`

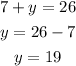
Therefore, there are;

7 Dimes and 19 Quarters

`\begin{gathered} x=7 \\ y=19 \end{gathered}`