Answer:
y^2/ 25 - x^2 / 9 = 1
Explanation:
Th standard form of a hyperbola is
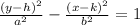
where (h,k ) are the coordinates of the centre and a and b are two constants.
The coordinates of the vertices are

and the equation of the asymptote is
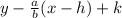
Now, the coordinates of the center for our hyperbola are (0,0); therefore,
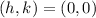
and the coordinates of the vertices we get from the graph are
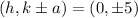
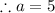
Finally, the equation for the asymptote we get from the graph is
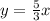
meaning

Hence,
h = 0,
b = 0,
a = 5,
b = 3
thereofore, the equation of the hyperbola is
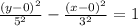
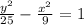
which is our answer!