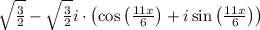SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given expression
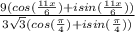
STEP 2: Simplify the expression
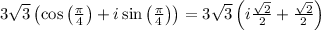
STEP 3: Rewrite the expression
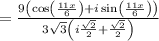
Divide the numbers:
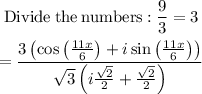
STEP 4: Apply Radical rule
![\begin{gathered} \mathrm{Apply\:radical\:rule}:\quad \sqrt[n]{a}=a^{(1)/(n)} \\ √(3)=3^{(1)/(2)} \\ =\frac{3\left(\cos \left((11x)/(6)\right)+i\sin \left((11x)/(6)\right)\right)}{3^{(1)/(2)}\left(i(√(2))/(2)+(√(2))/(2)\right)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yjjp285av3a851qkk7ayihh4e3xfb6rxmo.png)
STEP 5: Apply Exponent rule

STEP 6: Apply Radical rule
![\begin{gathered} \mathrm{Apply\:radical\:rule}:\quad \:a^{(1)/(n)}=\sqrt[n]{a} \\ 3^{(1)/(2)}=√(3) \\ =(√(3)\left(\cos \left((11x)/(6)\right)+i\sin \left((11x)/(6)\right)\right))/((√(2))/(2)+i(√(2))/(2)) \\ \text{By Multiplication,} \\ i(√(2))/(2)=(√(2)i)/(2) \\ =(√(3)\left(\cos \left((11x)/(6)\right)+i\sin \left((11x)/(6)\right)\right))/((√(2))/(2)+(√(2)i)/(2)) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qw7k4pkkhvoatefpyt6a6rqguv7di2l2eh.png)
STEP 7: Combine the fractions
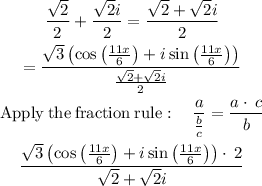
STEP 8: Factor out common term
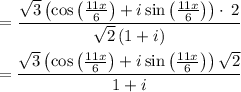
By simplification,
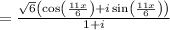
STEP 9: Rationalize
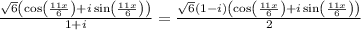
STEP 10: Write the answer in the required form
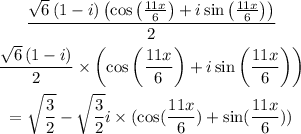
ANSWER: