Question

For a moving object, the force acting on the object varies directly with the object's acceleration. When a force of 56 N acts on a certain object, the accelerationof the object is 8 m/s?. If the acceleration of the object becomes 3 m/s?, what is the force?

Answer 1

STEP 1

Establish relationship between force and acceleration.

From the 1st statement, there is a direct variation between the force and the acceleration. This is put mathematically as

`F\text{ }\alpha\text{ a}`

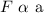
We introduce a constant, m

`\begin{gathered} F\text{ = ma where} \\ m\text{ is the proportionality constant creating the relationship thus } \\ Nperm/s^2\text{ as its unit} \end{gathered}`

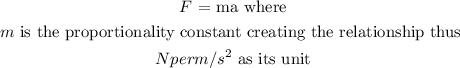
STEP 2

Derive value for the constant, m

`\begin{gathered} F\text{ = ma} \\ \text{Dividing both sides by a, we have} \\ (F)/(a)=m \\ where\text{ }f=56N,m=8m/s^2 \\ m=(56)/(8)=7Nperm/s^2=7Ns^2\text{ / m} \end{gathered}`

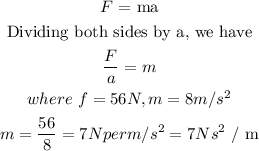
STEP 3

Apply this value of m to solve related equations.

`\begin{gathered} \text{where a = 3m/s}^2\text{ and m = }7Ns^2\text{ /m} \\ \text{and F = ma = 3 x 7 = 21}N \end{gathered}`

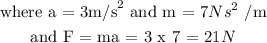
Thus, the force when acceleration becomes 3 m/sq seconds is 21 N