Question

Hancox Homes is a popular construction company that builds affordable housing. When the company first started, they sold 1 home the first month, 3 homes the second month, 9 homes the third month, and 27 homes the fourth month. DESCRIBE THE PATTERN THEN REPRESENT THE SEQUENCE AS A NUMERIC SEQUENCE AND A TABLE OF VALUE

Answer 1

The pattern is given below

1, 3, 9, 27

We can clearly see that the terms are indeed the powers of 3

i.e

`\begin{gathered} 3^0\text{ = 1} \\ 3^1\text{ = 3} \\ 3^2\text{ = 9} \\ 3^3\text{ =27} \end{gathered}`

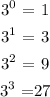
looking closely at the sequence generated, we can show that it follows the geometric sequence as

`r\text{ = }(T_2)/(T_1)\text{ = }(T_3)/(T_2)\text{ = }(T_(n+1))/(T_n)`

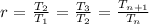
Thus, the common ratio r equals

`r\text{ = }(3)/(1)\text{ = }(9)/(3)\text{ = }(27)/(9)\text{ = 3}`

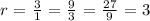
for any two consecutive numbers in the sequence

Hence, we can express the sequence as a numeric sequence thus:

`\begin{gathered} \text{Recall that T}_n=ar^(n-1) \\ T_n=(1)(3)^(n-1) \\ T_n=3^(n-1) \end{gathered}`

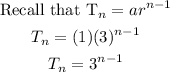
We can also create a table of values to show that this sequence follows the geometric sequence