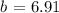Question

If the height of a gable end of a roof is 7.5 m and the rafters are 10.2 long, at what angle do the rafters slope, and how wide is the gable end at the base?

Answer 1

Consider the following diagram of the problem situation:

We need to find the angle alpha and the base b. To find the angle alpha, we can apply the following trigonometric identity:

`\sin (\alpha)=(h)/(l)`

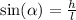
Replacing the data of the problem in the above equation, we get:

`\sin (\alpha)=(7.5)/(10.2)`

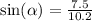
now, applying the inverse function of the sine function, we get:

`\alpha=\sin ^(-1)((7.5)/(10.2))=\text{ 47.33}`

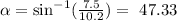
then, the angle would be:

`\alpha=47.33^(\circ)`

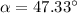
On the other hand, to find the lenght of the base, we can apply the Pythagorean Theorem:

`b\text{ = }\sqrt[]{l^2-h^2}\text{ = }\sqrt[]{(10.2)^2-(7.5)^2}\text{ = 6.91}`

so that, we can conclude that the base measures:

`b\text{ = 6.91}`