ANSWER:
As the value of B increases, the period of the function decreases, and the frequency of the function increases. When the value of B is negative, the graph of the function reflects over the x-axis
Explanation:
The period of a trigonometric function is given by the following equation:
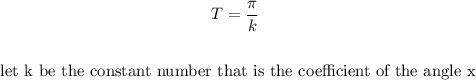
In this case, k is equal to B, if B increases then the period decreases, and since the frequency is inversely proportional to the period it would increase.
If the value of B is negative we would have the following:
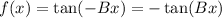
Therefore, there is a reflection on the x-axis.
As the value of B increases, the period of the function decreases, and the frequency of the function increases. When the value of B is negative, the graph of the function reflects over the x-axis