Solution:
Given:
The volume of water only:
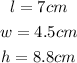
Using the formula;
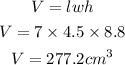
The volume of water and ring (height of water changes:
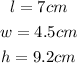
Using the formula;
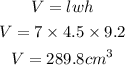
The volume of the gold ring is the difference in volumes.
Hence;
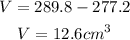
Therefore, the volume of the gold ring is 12.6 cubic centimeters.